The Application of LAMP

LAMP assumes the future is nothing more than the sum total of all interactions of "free will," both on an individual and international scale. While not an infallible method for predicting the future, LAMP gives the analyst a more powerful method for organizing all available information based on the perceptions of the national actors and uses it to make relevant predictions as to which alternate future is most likely to occur at a given moment in time. This part of the LAMP Portal provides a brief discussion of the 12 steps of LAMP and showcases the technique's use in predictive analysis.

LAMP differs in kind from other analytical techniques in that it is based on determining the relative probability of a series of alternate futures, rather than attempting to determine the quantitative probability of their occurrence. For a short PowerPoint presentation about LAMP, see The Lockwood Analytical Method for Prediction (LAMP).

The 12 steps of LAMP are as follows:

1. Define the issue for which you are trying to determine the most likely future.

This is an extremely important step in the LAMP method. If the issue is too broad, the analyst has too many actors and courses of action to consider, causing the number of alternate futures to explode exponentially. If the issue is vaguely defined, then the analyst ends up conducting too general an analysis. This makes subsequent comparisons of alternate futures less reliable. Examples of specific issue questions lending themselves to the LAMP are:

  1. How will the nuclear weapons issue affect relations among the four "nuclear republics" of the former Soviet Union?
  2. How will North Korea's emergence as a nuclear power affect nuclear proliferation in Southeast Asia?
  3. What is the likely involvement of Eastern European nations in the Bosnian conflict?

2. Specify the national "actors" involved.

The analyst should then determine the number of national "actors" who can directly affect this issue. For example, immediately following the collapse of the Soviet Union, the four so-called "nuclear republics" (Russia, Ukraine, Belarus, and Kazakhstan) were "actors" in the nuclear weapons issue because they had courses of action involving nuclear proliferation or armed conflict. Other republics within the former Soviet Union were not included because they did not have courses of action open to them to directly affect the future in this regard.

If the analyst is careful enough to limit the scope of his or her initial question, the number of "actors" involved should be no more than 5 or 6. If it is more than this, the number of possible "alternate futures" may become unmanageable. Unless the analyst has programmed the LAMP into computer software, it will not be easy to handle the large number of permutations that arise.

3. Perform an in-depth study of how each national actor perceives the issue in question.

This step involves the greatest amount of historical research for the analyst, and is the most time-consuming. Not only should the analyst examine current history from the national actor's viewpoint, but should also look for historical events, cultural factors, and even nuances of language that might have an impact on a nation's outlook. Failure to conduct an adequate perceptual study increases the danger that analysts will fall into the "mirror-imaging" trap of substituting their own logic for the national actor's. If this occurs, it skews the analyst's calculations when comparing the likelihood of the various "alternate futures," yielding less reliable predictions.

4. Specify all possible courses of action for each actor.

After completing the perceptual study of each actor, the possible courses of action should become apparent to the analyst. The analyst should not exclude a course of action merely because it seems unlikely that an actor will choose it, although choices should be excluded that are clearly impossible or beyond the strength of the actor in question. In my 1993 research project for example, for each of the three "breakaway" republics of Ukraine, Belarus, and Kazakhstan, there were three general courses of action which they could follow with respect to nuclear weapons:

  1. Continue Disarmament. The republic in question continues the process of becoming a "nuclear-free" state by ratifying the START and NPT agreements and carrying out their provisions.
  2. Pursue Independent Nuclear Capability. The republic decides to acquire the technology and resources necessary to produce its own nuclear weapons and associated delivery systems independent of the Russian systems located on its territory.
  3. Seize Soviet Nuclear Weapons. The republic decides to seize the nuclear weapons on its territory, either for establishing its own independent nuclear capability or to forestall any Russian attempt to preemptively seize such weapons.

For Russia, of course, there were two basic options:

  1. Continue Disarmament. Russia continues to work for the peaceful transfer of all nuclear weapons back under its control.
  2. Seize Soviet Nuclear Weapons Within the Republics. Under this course of action, Russia takes military action to seize control of the nuclear arsenals within one or more of the three breakaway republics.

5. Determine the major scenarios within which you compare the alternate futures.

One purpose of a scenario is to provide the major assumption which influences the actions of all national actors concerned. Often it is based on the actions of a major power outside the scope of an analyst's initial study. The other purpose, equally as important, is to give the analyst a means of limiting the potential number of actors for his problem. Applying the scenario approach to our nuclear republic problem, there were three possible scenarios. These scenarios were based on the likely future actions or conditions pertaining to our fourth nuclear republic, Russia, and were as follows:

  1. Russian Reformist Government Stays in Power. This scenario assumes Yeltsin is able to remain in power and successfully fend off the challenge posed by the ultra-nationalists under Zyuganov or Zhirinovskiy. Russia will continue to pursue its goal of unified control of the former Soviet nuclear arsenal by diplomatic means, and will not resort to military force.
  2. Ultra-Nationalist Government Seizes the Power in Russia. This scenario assumes Yeltsin is overthrown or voted out of power by an ultra-nationalist coalition, but that the new government does not immediately undertake military action to seize any of the nuclear arsenals in the other three republics.
  3. Ultra-Nationalist Government Moves to Seize Nuclear Arsenals. This scenario assumes a Russian ultra-nationalist government decides that it cannot afford to wait for events to run their course regarding disarmament, and undertakes immediate military action to seize the nuclear weapons in one or more of the three breakaway republics.

6. Calculate the total number of permutations of possible "alternate futures" for each scenario.

Here is where the necessity of limiting the number of actors and choices becomes most apparent. The general formula for computing the number of alternate futures is:

XY=Z

Where X equals the number of courses of action open to each actor, and y equals the number of national actors involved (assuming each actor has the same number of courses of action open to it), Z equals the total number of alternate futures to be compared. For example, if the analyst is looking at five actors with two courses of action open to each, then he or she is looking at only 32 alternate futures. If however, the analyst includes another national actor with three courses of action, then the number of alternate futures becomes 96. However, if there were three courses of action open to all five national actors, then the number of possible alternate futures explodes to 243!

Obviously, the use of a scenario helps the analyst keep the problem within manageable bounds.

For our nuclear republics problem, since there were three "national actors," Ukraine, Belarus, and Kazakhstan, and we are concerned with three courses of action open to each republic, the alternate futures work out as follows:

  1. Russian Reformist Government Stays in Power. Based on the number of possible courses of actions open to the three breakaway republics, there are 27 possible futures which can occur under this scenario.
  2. Ultra-Nationalist Government Seizes the Power. Again, based on the number of possible courses of action open to the breakaway republics, there are 27 possible futures which can occur under this scenario.
  3. Ultra-Nationalist Government Seizes Nuclear Arsenals. If we assume a Russian seizure of any of the outlying nuclear arsenals effectively preempts that republic's course of action, then there are 37 possible combinations of actions (and therefore 37 possible futures) which can arise within this scenario. If, however, we assume Russia's choice between its two courses of action will occur in competition with those of the targeted republic, then the number of alternate futures becomes 54.

7. Perform a "pairwise comparison" of all alternate futures within the scenario to determine their relative probability.

A "pairwise comparison" analyzes the alternate futures two at a time, always assuming the two futures being compared at the moment are the only ones that exist. For example, all futures within scenario 1 for the CIS nuclear republics are numbered 1 through 27. Future number 1 is compared to Future number 2. Based on all of the information the analyst is aware of at that moment, whichever future is deemed "more likely to occur" is given one vote. Future number 1 is then compared to all futures within the scenario. This continues until the analyst has compared and voted on the last pair of futures, numbers 26 and 27. This process repeats for the other scenarios.

The total number of votes is a function of the number of alternate futures to be analyzed, which in turn is a function of the number of actors and courses of action the analyst has determined for the issue. The formula for the number of pairwise comparison is:

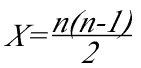
Mathematical Equasion

Where n equals the total number of alternate futures to be analyzed, and X equals the total number of pairwise comparisons. In a simple example, the number of pairwise comparisons on the four scenarios within The Russian View of US Strategy is X=4(4-1)/2=12/2=6.

However, as we increase the number of actors and courses of action involved, it is apparent how quickly the size of the problem can become unmanageable without either computer support or a prior decision on the part of the analyst to limit the scope of the analysis. For the nuclear republics problem, the number of pairwise comparisons for Scenario I was 27(27-1)/2, or 351 votes. For Scenario III, if we assumed 37 alternate futures, the number of pairwise comparisons required becomes 666. If we assumed there was 54 alternate futures, however, the number mushrooms to 1431 for this scenario alone!

As the analyst proceeds through the pairwise comparison, he or she discovers some "pairs" are easier to vote on then others. For example, based on a perceptual study, the analyst may well conclude that scenarios in which Belarus continues disarmament under the conditions of Scenario I are more likely than those in which it seizes the nuclear weapons themselves. And yet the analyst is soon confronted with the following pair of alternate futures:

These two alternate futures were clearly among the most "bizarre" possible futures, since evidence in 1993 indicated virtually no likelihood of Belarus seizing nuclear weapons. The problem is not all that difficult, however, since both futures assumed identical courses of action for Ukraine and Belarus. The only real difference in these futures was whether Kazakhstan developed independent nuclear capability or seized its nuclear weapons. Since the completion of this project in 1993, both Kazakhstan and Belarus have surrendered their nuclear weapons, narrowing the potential range of alternate futures to 12.

Likewise, the analyst has a relatively easy time with comparing alternate futures at opposite ends of the scale of relative probability, such as the following example:

Here the choice of Future X over Future Y is much easier, even though there are no courses of action common in either future. This is because of the perceptual study the analyst has undertaken prior to the vote, making a future in which Ukraine pursues independent nuclear capability certainly more plausible than one in which both Belarus and Kazakhstan seized their respective nuclear weapons.

8. Rank the alternate futures for each scenario from highest relative probability to the lowest based on the number of "votes" received.

What you have at the end of the pairwise comparison is a series of futures receiving different numbers of votes based upon their relative probability to each other. The analyst then rank-orders the futures from "most likely" to "least likely" based upon the number of votes received.

9. Assuming each future occurs, analyze each alternate future in terms of its consequences for the issue in question.

This step requires some imagination on the part of the analyst; he is, after all, writing "future history" of things that might be, given that the national actors take the courses of action of a particular alternate future. In the nuclear republics, each example of the alternate futures is summarized in a separate section which answers the following question: What are the consequences of this particular future for arms control, nuclear nonproliferation, and the likelihood of armed conflict? Depending on the prediction issue and the degree of research the analyst is willing to undertake, describing the consequences of a given alternate future often takes longer than one or two paragraphs.

10. Determine the "focal events" that must occur in our present in order to bring about a given alternate future.

This step is not addressed in the consequences paragraph, since the analyst must thoroughly examine the consequences of an alternate future and its potential for transposition. A "focal event" is an occurrence of sufficient magnitude that it changes the relative probability of alternate futures. If we were to "draw a line" in time from our present into the future, a focal event would resemble an intersection with two or more branches into other futures. Once the path is taken, we would soon be confronted with a different array of possible futures and branching off points. The most likely future has the fewest focal events leading into it; it is the alternate future offering the line of least resistance. In fact, our present might so closely resemble the alternate future that no focal events occur.

The more "bizarre" futures, on the other hand, have more focal events leading to them, since more such events are required in order to change our present into those futures. For the analyst, these are the alternate futures receiving the fewest votes during the pairwise comparison in Step 7 of LAMP.

11. Develop indicators for the focal events.

As the next-to-last step in the LAMP process, this step links the LAMP technique with the more familiar Indications and Warning process. For each focal event associated with an alternate future, it should be possible to develop a list of indicators that such an event either has occurred or is about to occur. Once these indicators are entered into an automated database along with the focal events and alternate futures, the analyst has almost completed the basic 12-step LAMP process. Subsequent activity consists of periodic "revoting" of the alternate futures as new information is acquired, refinement of the indicators associated with particular focal events, as well as the identification of additional focal events for the more exotic alternate futures.

12. State the potential of a given alternate future to "transpose" into another alternate future.

The concept of "transposition" is familiar to chess players as it pertains to chess opening theory. Transposition occurs when one chess opening's line of play leads into one resembling a different chess opening. The same occurs in our array of alternate futures. Since every act of free will changes the future, it has virtually the same result as transposition does in chess. Once the analyst has described the consequences of an alternate future, its potential for transposition into another alternate future should be noted, since this may affect the relative probability of these futures.